
Biocomplexity:
Adaptive Behavior in Complex Stochastic Dynamical Systems
Biosystems 59 (2001) 109-123
Walter J. Freeman(1) , Robert Kozma(1,2) , and Paul J. Werbos(3)
(1)University of California at Berkeley, Department of Molecular and Cell Biology
LSA 142, Berkeley, CA 94720-3200, Email: wfreeman@socrates.berkeley.edu
(2)University of Memphis, Department of Mathematical Sciences
373 Dunn Hall, Memphis, TN 38512, Email: rkozma@memphis.edu
(3)National Science Foundation(*), Room 675
4201 Wilson Blvd., Arlington, VA 22230, Email: pwerbos@nsf.gov
(*)The views expressed herein are the personal views of the author and do not reflect the views of NSF or the US Government.
Key Words: Non-autonomous dynamical system, Chaotic resonance, Stochastic resonance, KIII model, Chaotic neurodynamics, Destabilization of the sensory cortex.
Summary
Existing methods of complexity research are capable of describing certain specifics of biosystems over a given narrow range of parameters but often they cannot account for the initial emergence of complex biological systems, their evolution, state changes and sometimes abrupt state transitions. Chaos tools have the potential of reaching to the essential driving mechanisms that organize matter into living substances.
Our basic thesis is that while established chaos tools are useful in describing complexity in physical systems, they lack the power of grasping the essence of the complexity of life. This thesis is illustrated by sensory perception of vertebrates and the operation of the vertebrate brain. The study of complexity, at the level of biological systems, cannot be completed by the analytical tools that have been developed for non-living systems. We propose a new approach to chaos research that has the potential of characterizing biological complexity. Our study is biologically motivated and solidly based in the biodynamics of higher brain function. Our biocomplexity model has the following features:
1) it is high-dimensional, but the dimensionality is not rigid, rather it changes dynamically;
2) it is not autonomous and continuously interacts with and communicates with individual environments that are selected by the model from the infinitely complex world;
3) as a result, it is adaptive and modifies its internal organization in response to environmental factors by changing them to meet its own goals;
4) it is a distributed object that evolves both in space and time toward goals that it is continually re-shaping in the light of cumulative experience stored in memory;
5) it is driven and stabilized by noise of internal origin through self-organizing dynamics.
The resulting theory of stochastic dynamical systems is a mathematical field at the interface of dynamical system theory and stochastic differential equations. This paper outlines several possible avenues to analyze these systems. Of special interest are input-induced and noise-generated, or spontaneous state-transitions and related stability issues.
1) Introduction
The development of the theory of chaos in the past two decades has suggested a resolution of the discrepancy between mesoscopic (Freeman, 2000a) global order and aperiodic seemingly random activity at microscopic levels. In particular, models of deterministic chaos have been proposed, such as twist-flip maps and the Lorenz, Rössler, and Chua attractors, which are capable of dramatic and yet fully reversible changes in their aperiodic outputs with small changes in their bifurcation parameters. However, these models are low-dimensional, stationary, autonomous, and essentially noise-free, so they are ill-formed to model brains, which fail to conform to any of these conditions. Attempts to measure correlation dimensions, Lyapunov exponents, and related numeric features of brain subsystems have failed to yield normative results and have fallen into disrepute (Rapp 1993).
However, deterministic chaos governs only a small subset of chaotic systems. Another large class is opened by reaction-diffusion equations, which includes chemical morphogenesis (Turing, 1952) and irreversible thermodynamics (Prigogine, 1980) giving "order from disorder". These models also fail, primarily because the axon with its propagated action potential is an early phylogenetic adaptation in multicellular animals that surmounts the limitations of transmission by diffusion. At the price of a delay, an axon distributes the resultant of dendritic integration by a neuron not only without attenuation but commonly with amplification in proportion to the number of branches. The diffusion term is appropriate for modeling axodendritic cables and synapses over transmission distances < 1 mm, but it is not appropriate in models of the interactions within neural networks and populations. For similar reasons, models based in hydrodynamics and turbulence are unsatisfactory; there is nothing equivalent to viscosity or to molar convection in neurodynamics. Terminal chaos (Zak, 1993) is implemented in digital models of dynamical systems by randomization of the terminal bits of rational numbers in difference equations (representing real numbers in differential equations), where it lessens some of the rigidity of digital embodiments that impairs their utility for representing chaotic systems (Freeman et al., 1997). The best available models are those from synergetics, including the laser of Haken, who described microscopic particles as being "enslaved" by a macroscopic "order parameter" in a relationship of "circular causality" (Haken, 1991).
Even casual inspection of time series derived by sampling and recording from the fields of electroencephalographic (EEG) and magneto-encephalographic (MEG) potential generated by active brains reveals continuous widespread oscillations. These waves suggest the overlap of multiple rhythms embedded in broad-spectrum noise. In dynamical terms they might be ascribed to limit cycle attractors, because spectral analysis of short segments reveals peaks in the classical frequency ranges of the alpha (8-12 Hz), theta (3-7 Hz), beta (13-30 Hz) and gamma (30-100 Hz) bands of the EEG and MEG. However, autocorrelation functions go rapidly to zero, and the basic form to which spectra converge, as the duration of segments chosen for analysis increases, is a linear decrease in log power with increasing log frequency at a slope near 2 ("1/f2").
This form is consistent with Brownian motion and telegraph noise. The unpredictability of brain oscillations suggests that EEGs and MEGs manifest either multiple limit cycle attractors with time variance by continuous modulation, or multiple chaotic attractors with repetitive state transitions, or time-varying colored noise, or all of the above. In all likelihood these fields of potential are epiphenomenal, probably equivalent to the sounds of internal combustion engines at work, or to antique computers in science fiction movies, or to the roars of crowds at football games. In fact, most neuroscientists reject EEG and MEG evidence, in the beliefs that the real work of brains is done by action potentials in neural networks, and that recording wave activity is equivalent to observing an engine with a stethoscope or a computer with a D'Arsonval galvanometer. However, one can learn a lot about a system by listening and watching, if one knows what to seek and find. This is the main direction of the research described in this paper.
2. Models of Spatio-Temporal Chaos
Per definition, in chaotic systems infinitesimal variations in the initial conditions are quickly amplified and lead to divergent behavior with respect to the unperturbed state. Computational chaos studies in the past few decades have been concentrated on high-accuracy computations and the identification of parameters ranges, attractor basins, where the nonlinear system converges to an attractor. In this approach noise causes divergence and, therefore, it is undesirable. Noise, however, is an inevitable component of any real life system, both physical and biological. Our proposal is an assay to resolve this contradiction between computational/theoretical models of complexity and real life by analyzing noisy dynamical systems and showing that noise plays a key role in the emergence of biological complexity, and in maintaining its stability over various temporal and spatial scales.
2.1 Discrete Spatial and Temporal Mappings: Coupled Map Lattices
Spatio-temporal dynamics of complex, nonlinear systems has been studied intensively during the recent years, including fluid flow, crystal growth, coupled optical systems, evolutionary information processing, neuro-dynamics, etc. In modeling such systems, coupled map lattices (CMLs) utilize continuous state-space and discrete time and space coordinates (Kaneko, 1990, 1993; Perez et al., 1992). Lattice elements in a CML are obtained by coarse-graining the original microscopic quantities. Coarse-grain models represent a connection between the microscopic world and macroscopic observations and correspond to the level of our knowledge about the investigated processes. Finding the proper coarse-graining to the description of an actual physical, biological, economical, etc. system is a very important and still not completely resolved question. The theoretical study of systems of coupled map lattices is one possible avenue of modeling stochastic effects in chaotic systems. Coupled map lattice theory grew out of studies on collective movements of coupled oscillators. CMLs with local, direct-neighbor coupling can be regarded as approximations to the diffusion process. The globally coupled maps are related to mean-field interactions. Equations of the Coupled Map Lattice model are given in Appendix A.
In locally and globally coupled lattices various types of temporal behaviors have been described, ranging from fixed points and limit cycles to collective quasi-periodic and chaotic oscillations (Kaneko, 1993; Csilling et al., 1994; Chate, 1995; Chate et al., 1996). The presence of low-dimensional collective behaviors in spatially extended systems is a controversial issue. Contrary to earlier theoretical studies predicting the absence of global collective behaviors in the case of semi-localized coupling, quasi-periodic collective dynamics has been observed in such systems (Chate and Manneville, 1992; Sinha et al., 1992). Further studies showed that the onset of macroscopic collective behavior can be attributed to the window structure of the bifurcation maps (Perez et al., 1993).
Intermediate coupling is closely related to the topology of the physical space and it plays a crucial role in solving practical problems. Until now, however, relatively small attention is paid to intermediate-range effects due to the complexity of the required analysis. Pioneering works in this field include studies on spatial correlations based on coupled Ginzburg-Landau-type oscillators and investigations on the effect of higher spatial dimensionality on the collective behaviors, (Chate et al., 1996; Kuramoto and Nakao, 1996, 1997). In the field of neuro-dynamics it has been realized only very recently that network architectures with non-local connectivity and adaptive structure are key elements of emergent intelligence in neural networks in the form of high-level symbolic knowledge, causal reasoning and symbolic rules (Kozma et al., 1996; Kozma, 1997). Results obtained with studying intermediate-range coupling in CMLs are directly related to the emergence of intelligent behavior in neural networks and can be utilized in models of intelligent information processing (Kozma, 1998; Gade and Hu, 1999).
Phase diagrams are very useful tools in dynamical system studies as they express the relationship between the control parameters and the state of the system. Phase diagrams can exhibit a wide variety of attractors, Kaneko (1997, 1998). Coherent attractor: all the units are moving along the same trajectory. A single attractor covers the space, i.e. the behavior of the system is completely in synchrony. This is a typical state with strong coupling (i.e. large epsilon) and small values of nonlinearity control parameter (small alpha). For details of notations, see Appendix A. Ordered phase: the system falls into a given number of frozen attractors. The number of clusters varies depending on the control parameter values. The attractor basin corresponding to 2-cluster frozen attractors is the largest, and it decreases with increasing cluster numbers, 2, 4, 8, 16, ... With increasing epsilon the border between the attractor basins is becoming increasingly fuzzy and mixed areas are produced. Partially ordered phase (intermittent and glassy): the trajectories may fall into a large number of clusters in some cases, or into a small number of clusters, depending on the initial conditions. Turbulent phase: each unit follows a separate trajectory. Turbulent phase arises for weak coupling and for large values of the control parameter alpha. In this case the system is completely fragmented and chaos dominates over ordered behavior. Ishii uses cluster frozen attractor region from the ordered phase for information storage and retrieval. The system shows significantly improved memory capacity (per node) compared to Hopfield learning and the classification performance is also better in most of the pattern classification problems introduced (Ishii, 1996).
Phase transitions induced by noise in coupled map lattices have been studied by several authors. It has been shown that in some models the entropy of the lattice states versus the intensity of the noise has a resonance character (Sbitnev, 1997; Sinha, 1998). At the state transition point, the complexity induced by an external sub-threshold (periodic) signal reaches a maximum value. CMLs are excellent modeling domains to analyze synchronization effects and various chaos control strategies in noisy environment, (Konno et al., 1996), (Roy and Amritkar , 1997; Schuster and Stemmler, 1997).
Stochastic resonance (SR) is an interesting application of noisy dynamical systems for information processing. SR has become a well-established research field during the past two decades and it is widely applied in various disciplines, from laser physics, semiconductor devices, through neurophysiology, to population dynamics. SR effects can arise in a bi- or multi-stable system with an energy threshold between the states. External or internal noise can initiate a transition between the states. This effect has a resonance character and it can be used to enhance a weak (periodic) input signal, thus producing a high signal-to-noise ratio (Gammaitoni et al., 1998; Assumian et al., 1998). There are numerous examples of successful implementation in neural systems (Moss and Pei, 1995; Bulsara et al., 1991; ChapeauBlondeau and Godivier, 1996; Levin and Miller, 1996; Mitaim and Kosko, 1998). It is very likely that brains use resonance effects in a more subtle way than it is suggested by the original SR theory. Chaotic resonance (CR) is a phenomenon that has been introduced recently for the description of stochastic effects in high dimensional nonlinear systems and has been used for the analysis of neural systems (Brown and Chua, 1999; Kozma and Freeman, 2001).
2.2 Information Encoding in Chaotic Attractors
Now let us address the question of information coding in aperiodic (chaotic) attractors. We leave the safe and thoroughly explored territory of equilibrium and bifurcation schemes that use fixed point based encoding. This is a great leap into the non-equilibrium dynamics of unstable periodic orbits. The complexity of the problems seems overwhelming, if not intractable and the intellectual challenge is indeed enormous. There is, however, hope that we can meet this challenge because we know existing systems working on this principle: brains. The seminal paper by Skarda and Freeman gives a comprehensive account of spatio-temporal effects in brains using methods of dynamic system theory and chaos (Skarda and Freeman, 1987). Numerous studies in various laboratories are conducted to harness the principle of chaotic encoding for understanding brain dynamics (Babloyantz and Destexhe, 1986; Tsuda, 1992, 1994; Schiff et al., 1994; Aradi et al., 1995).
Motivated strongly by these neurophysiological observations, intensive research is conducted in the field of computational NNs utilizing chaotic encoding in software and hardware embodiment. In NN implementations, an array of nonlinear processing elements with recurrent connections can be used. A one-dimensional array of elements with piece-wise linear characteristics is used by Andreyev with no connections between the elements inside the array (Andreyev et al., 1996). Intensive research efforts have been conducted to understand theoretical and practical issues concerning chaotic neural networks (Aihara et al., 1990; Perrone and Basti, 1995; Wang, 1996; Schuster and Stemmler, 1997; Borisyuk and Borisyuk, 1997; Nakagawa, 1998; Minai and Anand, 1998). In a separate development Freeman's KIII nets have been introduced which represent a prototype of dynamic memory devices based on encoding in aperiodic (chaotic) attractors (Freeman, 1992).
Small stochastic fluctuations in the state of the system play an important role in biological neural networks when each neuron typically receives synaptic input from thousands of other neurons within the radius of its dendritic arbor. It gives synaptic output to thousands of others within the radius of its axon, and not the same thousands because each neuron connects with less than 1% of the neurons within its arbors, owing to the exceedingly high packing density of cortical neurons. These properties of dense but sparse interconnection of immense numbers of otherwise autonomously active nonlinear neurons provide the conditions needed for the emergence of mesoscopic masses (Freeman, 2000a), ensembles, and populations, which have properties related to but transcending the capacities of the neurons that create them. The most significant property of ensembles is the capacity for undergoing rapid and repeated global state changes (Freeman, 2000b). Examples are the abrupt reorganizations manifested in the patterns of neural activity in the brain and spinal cord by the transitions between walking and running, speaking and swallowing, sleeping and waking, and more generally the staccato flow of thoughts and mental images. These pattern changes on a massive scale appear to be incompatible with systems that are dominated by noise, such as hot plates, decaying vegetation and unruly crowds.
This self-sustaining, randomized, steady state background activity is the source from which ordered states of macroscopic neural activity emerge. The brain medium has an intimate relationship with the dynamics through a generally weak, sub-threshold interaction of neurons. The synaptic interactions of neurons provide weak constraints on the participants, and the resulting covariance appears in the form of spatiotemporal patterns of EEG and MEG (Freeman and Kozma, 2000). The degree of covariance is low, and the shared patterns would be inaccessible by other parts of the forebrain and brainstem, if the output pathways from self-organizing cortices conformed to the topographic order of the input pathways to most primary sensory cortices. This is not the case for the output path of the olfactory bulb, which is a divergent-convergent projection that performs a spatial integral transformation on bulbar activity before it is delivered to the targets of bulbar transmission, and the broad receptor fields in the targets of neocortical outputs give reason to believe that they undergo comparable integral transforms through similarly divergent pathways. If this proves to be the case, then it follows that unit activity is the best measure of cortical inputs, and that EEG and MEG potentials provide the best measure of cortical outputs, because the volume conductor performs a similar spatial integration on the dendritic potentials of local neural neighborhoods.
3. Biologically motivated KIII model of sensory dynamics
3.1 Architecture of the KIII model
Theoretical foundations of the KIII model have been laid down by Freeman in the early 70’s (Freeman, 1975). Freeman introduced a family of neuronal assemblies and called them the K0, KI, KII, and KIII sets. The name itself, i.e. K-sets, has been chosen to honor Katchalsky, a pioneer of studies on the collective behavior of neuron populations. The KO basic unit describes a dynamic behavior using 2nd order ordinary differential equations based on open-loop characteristics of neural masses. The KO set includes an asymmetric sigmoid function with a variable positive saturation level between 1 and 5. The negative saturation level is fixed at -1, (Freeman, 1975). By coupling a number of excitatory (E) or inhibitory (I) KO sets, KIE or KII are formed, respectively. The interaction of KIE and KII gives the KII set. Finally, coupling several KII sets with excitatory, inhibitory and feedback loops, one arrives at the KIII set. Details of the KIII model and its neuro-physiological foundations are given in the work of Freeman and co-workers (Yao and Freeman, 1990; Chang et al., 1998; Kozma and Freeman, 2000a).
The KIII model is an example of layered networks with nonlinear units having the following types of coupling: (i) feed-forward connections between layers, (ii) lateral excitation or inhibition across certain layers, (iii) feedback connections between layers. Decade-long studies indicate that this class of networks can exhibit a wide range of dynamical behaviors, i.e., fixed point and limit cycle attractors, quasi-periodic oscillations and chaos. KIII models can grasp the essence of the observed dynamical behavior in certain biological neural networks, including olfaction (Freeman 1992). In the KIII model of the olfaction the layers correspond to: receptors (R), periglomerular cells (P1 and P2), olfactory bulb (OB), anterior olfactory nucleus (AON), prepyriform cortex (PC) and deep pyramidal cells (C). There is a general feed-forward structure from R to P1 and OB, and from OB to AON and PC via the lateral olfactory tract (LOT). Lateral connections are incorporated at the OB at two levels while feedback is directed from PC to AON, from C to OB, and from AON to OB and P1 via the medial olfactory tract (MOT). Note that the OB, the AON and PC are all examples of interconnected KII sets.
3.2 Operation of the KIII memory
The operation of the KIII memory can be described as follows. In the absence of stimuli the system is in a high-dimensional state of spatially coherent basal activity. The basal state is described by an aperiodic (chaotic) global attractor. In response to external stimuli, the system can be kicked-off from the basal state into a local memory wing. This wing is usually of much smaller dimension than the basal state. It shows coherent and spatially patterned amplitude-modulated (AM) fluctuations. The system resides in this localized wing for the duration of the stimuli then it returns to the basal state. This is a temporal burst process having a duration of about a few 100 ms. A memory pattern is defined therefore as a spatio-temporal process represented by the sequence of spatial AM patterns during the burst.
The typical number of nodes in the KIII model is in the range of a few hundred, corresponding to an 8x8 array of nodes in a layer. The attractor landscape in this high-dimensional system becomes very complex. Previous computer simulations showed that in this case attractor crowding takes place, (Chang et al., 1998). In other words, the extension of the attractors diminishes and it becomes comparable to the resolution of the numerical computation on a digital computer. As a result, the trained KIII system is extremely sensitive to small variations in the parameters, which was responsible for its unsatisfactory generalization performance.
Attractor crowding is an unavoidable manifestation of the complexity of the high-dimensional chaotic KIII system. Highly evolved, fractured attractor boundaries are found, which produce a mixture of various attractors in a small neighborhood of a typical point of the state space. Recent research into the description of attractor ruins and Milnor attractors (Kaneko, 1998; Tsuda, 2001) could provide a mathematical tool to analyze our observations with KIII. The observed dominance of a small number of attractor states at a given moment of pattern retrieval is a manifestation of Haken's slaving principle. As the external conditions vary, the low-dimensional subspace into which the system collapses also changes. The consequences of such a complex attractor topology are illustrated on the example of KII subsets.
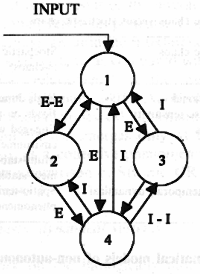
To understand the structure of the attractors, let us analyze first the behavior of a single KII set; see Fig. 1. There are 4 gain coefficients in a KII set. These are: WEE - the gain between excitatory nodes 1 and 2; WII - the gain between inhibitory nodes 3 and 4; WIE - the gain from excitatory to inhibitory nodes; and WEI - the gain between inhibitory and excitatory nodes. In this example, fixed-point asymptotic response is studied. The impulse response of the KII sets is decayed oscillation with possible excitatory or inhibitory bias, or with no bias in the asymptotic regime. The obtained attractor regions are shown in Fig.2a-c. In Figure 2, a 3D plot is given in the space of 3 gain coefficients (WEE, WII, WIE) while the value of the fourth gain (WEI) has been fixed. Some parameter values represent crisp attractor regions, but there are significant overlaps among the attractors, depending on the initial conditions. This behavior resembles the partially ordered phase-type attractors (glassy or intermittent) in globally coupled lattices, (Kaneko, 1990). There is an extended region where the unbiased attractor is dominant, see Fig. 2a. Also, the attractor region of the negative bias state shown in Fig. 2c is quite large. The positive bias state, however, is limited to a narrow tube only, as it is seen in Fig. 2b. Details of the attractors of KII and KIII sets are given in (Kozma and Freeman, 2001). Results in Fig. 2 indicate that the stability of KIII cannot be achieved by using a fine-tuned set of parameters. Instead, we must acknowledge the co-existence of a range of attractors in many actual realization of the system and build robust KIII dynamics in this way (Kozma and Freeman, 1999).
The emerging field of neural computation involves dynamics in many ways. Neural networks with a wide variety of activation dynamics were proved to be capable of one-pass on-line learning which stored sufficiently disparate arbitrary patterns as arbitrary attractors (Hirsch, 1989, 1996). In the KIII model, several learning tools are used. One is fast Hebbian learning of stimulus patterns. The other learning method is long-term habituation of background activity. Habituation can be modeled as incremental weight decay in the form of forgetting. A third mechanism involves nonlinear adaptive control techniques (Werbos, 1992) aiming at the stabilization of aperiodic trajectories. All these learning methods exist in a subtle balance and their relative importance changes at various stages of the memory process (Kozma and Freeman, 2001). Readout of the encoded information takes place at the mitral level from the spatially coherent AM patterns. We evaluate the input-induced oscillations in the gamma band (20 Hz to 80 Hz) across space. The change of the spatial AM pattern during the phase transition has been clearly observed. After the stimulus ceased, the activity returns to the basal state.
4. Mathematical models of non-autonomous dynamical systems
4.1 Noise effects in KIII
Noise has a special role in the KIII model. There are Gaussian noise components injected at different locations: at the input channels and also centrally at the AON. The input noise is spatially independent and rectified while the central noise in centrifugal and uniform in space with possible bias. Depending on the noise intensity and bias, resonance effects have been identified in the KIII model. Noise effects in KIII have certain similarity with stochastic resonance (SR) but they have very crucial differences (Kozma and Freeman, 2000b). Following earlier convention we will use the terminology Stochastic Chaos (SC) for the description of aperiodic behavior in brain dynamics which has been modeled by KIII (Freeman, 2000b; Werbos, 2000; Kozma and Freeman, 2001). Table I summarizes our present understanding on the relation between deterministic chaos and stochastic chaos.
Table I: Deterministic Chaos versus Stochastic Chaos
|
Deterministic Chaos |
Stochastic Chaos (s-chaos) |
|
Low dimensional |
High dimensional |
|
Extreme noise sensitivity |
Feeds on noise |
|
Autonomous |
Engaged with environment |
|
Stationary |
Multi-stable, meta-stable |
|
Typical in (temporal) dynamical systems |
Spatio-temporal phenomenon |
Table II: Stochastic Resonance versus Stochastic Chaos
|
Stochastic Resonance (SR) |
Chaotic Resonance (CR) |
|
Given bi- (multi-) stable nonlinear system |
Continuously changing multi-stable nonlinear system |
|
Weak (periodic) signal transmitted |
Fluctuating carrier signal of internal origin |
|
External and internal noise magnifies the input signal by de-stabilizing chaos |
Input and central noise stabilizes the system and amplifies the chaotic signals |
|
Maximum signal-to-noise ratio at a well-defined noise level (resonance) |
Maximum amplification at some intermediate noise level (resonance) |
|
Chaotic components |
Components are not chaotic and chaos is a collective feature |
Stochastic resonance has 3 main components: a bi- or multi-stable energy function, weak (periodic) input signal, and a noise component (Moss and Pei, 1995; Gammiatoni et al., 1998). The addition of noise in stochastic resonance models can enhance the signal-to-noise ratio, which is of great practical importance for signal processing applications of SR. The interaction of noise with the oscillatory signal has a resonance character in the KIII model as well. The oscillatory signal in the KIII model, however, is not coming from the external world, but it is the result of the interaction of the various internal KIII components. Therefore, the signal may have an intimate interference with the noise in a KIII system, as compared with the pure input/output relationship in the case of SR (Kozma and Freeman, 2001). Another difference is that individual nodes exhibit chaotic behavior in SR, while chaos emerges only at the macroscopic level, as a collective phenomenon in brain chaos. The comparison of SR and CR is summarized in Table II.
4.2 Stochastic dynamical systems
The work on the biologically motivated KIII model leads to a straightforward conclusion: we need to develop "stochastic chaos theory," a body of mathematics which does for their kind of model the same kind of service which ordinary chaos does for ODE models. The need for such a development seems extremely obvious. The real puzzle is why this body of mathematics does not exist, or why — if it exists in some form — it has not been collected together and unified and disseminated in the same way as ordinary chaos theory has been disseminated. Years ago, ordinary nonlinear system dynamics and chaos theory went through amazing tribulation and resistance to their development. In the early years, some mathematicians talked about the need for "qualitative theory of ODE." They emphasized the need to develop a new field of mathematics, complementary to the more traditional mathematics of ODE, to address questions about qualitative behavior which the earlier theory (however valuable) simply did not address, (Werbos, 2000). After decades of effort, nonlinear systems theory now provides a large and growing literature on the qualitative behavior of systems of the form
![]()
where x is a vector, W is a set of weights or parameters, and where ∂t is physics notation for differentiation with respect to time. The KIII model is not so far away from the earlier ODE formulations. It may be written schematically as
![]()
where e is a fairly small stochastic disturbance vector. In effect, Freeman has been pleading with mathematicians to provide an extension of chaos theory, to help him rigorously analyze the properties of models in this class. Based on biological principles, Freeman asserts that instead of the 1st order differential equation in the dynamical equations, one must use at least 2nd order differential equations (Freeman, 1975).
The main obstacle to the development of non-autonomous chaos theory seems to be a matter of historical circumstances. One group of mathematicians is committed to a probabilistic view of the world, and they prove theorems, which address questions analogous to those, which were addressed by the mathematics of ODE, before chaos theory was developed. Another group has spent their lives working with a deterministic version of chaos, and is often sympathetic to the view that "noise" should always be represented as the outcome of some underlying deterministic process. The challenge, in part, is how to settle new territory in the no-man’s-land between these groups, a land that no one has claimed as yet. These extreme alternatives do not fully address the needs of biology or of several other fields. Very often, the stochastic form given in Eq. (2) will be far more parsimonious (and easier to test) than a model which requires a detailed, explicit deterministic account of every source of microscopic or quantum noise which results in e. Likewise, from the viewpoint of pure mathematics, it is a reasonable and well-posed question to ask what the qualitative behavior of such a system would be.
The first suggestion, then, is to try to reproduce the achievements of chaos theory for this more general class of systems, particularly for the case where e is small. In formal terms, we have to write a Stochastic Differential Equation (SDE) (El-Karoui and Mazliak, 1997). The need here is for a more unified and comprehensive qualitative theory of SDE, analogous to the modern qualitative theory of ODE, capable at a minimum of assisting (and simplifying) the analysis of KIII-type models. The term "stochastic chaos theory" is the best term we can think of, in discussions between Kozma, Freeman and Werbos, (Werbos, 2000). Beyond this core body of mathematics, however, there is a need for other related types of mathematical tools here. Markov random fields are powerful tools that can help to enhance the analysis of spatio-temporal dynamics of KIII-type models.
4.3 Causality and spatio-temporal chaos in Markov random fields
The qualitative
theory of ordinary SDE would already address Freeman’s current concerns,
and might well provide a fully adequate foundation for computational neuroscience,
coupled with adaptive control techniques to be used in learning, adaptation
and stability control (Werbos, 1992). However, SDE themselves are a special
case of a larger class of systems. SDE assume that the random disturbance
"e(t)" is not correlated with ![]() This is called the "causality assumption" in statistics. (More precisely,
it is assumed that e(t) is statistically independent of prior
values of x and e.) Conventional time-series models,
formulated as x(t+1)=f(x(t),e(t)),
typically make the same assumption (Box and Jenkins, 1970). Note that e(t)
typically is correlated with
This is called the "causality assumption" in statistics. (More precisely,
it is assumed that e(t) is statistically independent of prior
values of x and e.) Conventional time-series models,
formulated as x(t+1)=f(x(t),e(t)),
typically make the same assumption (Box and Jenkins, 1970). Note that e(t)
typically is correlated with ![]() because random disturbances typically do change the state of the system at
later times.
because random disturbances typically do change the state of the system at
later times.
More recently, mathematicians have become interested in the formal properties of mixed forwards-backwards SDE. In such models, random disturbances can cause effects both at later times and at earlier times. They claim that such models are useful both in optimal control and in economics; for example, they may lead to capabilities very similar to those of Dual Heuristic Programming related to the Pontryagin equation (Werbos, 1994). Mixed forwards-backwards systems will be crucial to a more rigorous and concise reformulation of quantum field theory (Werbos, 1989, 1998, 1999; Zinn-Justin, 1996). There are certain critical experiments in physics — called "Bell’s Theorem" experiments — which are designed to demonstrate that causality actually runs forwards and backwards through time, symmetrically, at the microscopic level (Werbos, 1989; Penrose, 1994). The earliest papers on this were published by DeBeauregard and Werbos and later cited by (Penrose, 1994) among others, although Von Neumann’s classic tract on quantum mechanics clearly evinced a similar intuition.
If the physical universe we live in might actually be a mixed forwards-backwards system of some kind, then we need to understand the mathematics of such systems better than we now do. This is true, regardless of which formalism or theory survives future tests; indeed, deeper mathematical insight will be crucial to understanding the theories well enough to test them! Forwards-backwards SDE involves continuous time. To develop the mathematics, we may also consider the related issue of discrete time systems. The relevant time-forwards discrete systems can generally be written as x(t+1)=f(x(t),...,x(t-k),e), with the causality assumption applied to e. To define the forwards-backwards generalization of such systems, consider systems defined as Markov Random Fields (MRF) over the set of time points t = -∞,...., -2, -1,0,1,2,...,∞. We call this the "0+1-D" special case of a more general space-time MRF system (Werbos, 1998); the "0+1" refers to zero space dimensions and one time dimension.
The literature on space-like (n+0-D) MRFs is huge and diverse. It ranges from old discussions of lattice dynamics and spin-glass neural networks in physics, through to image processing technology, through to recent work by (Jordan, 1998) and others applying MRF mathematics to irregular lattices representing systems of propositions or "belief networks." Equations to introduce the MRF formalism are given in Appendix B.
For biology
and physics, a key research goal is to better understand the "arrow of
time" -- and then to understand the interface between microscopic forwards-backwards
symmetry and macroscopic time-forwards causality. This suggests one warm-up
question at the 0+1-D level: when can a given dynamical process be
represented equivalently as a time-forwards Markov process, as a time-backwards
Markov process, and as mixed forwards-backwards process? In the 0+1-D case,
when ![]() is taken from a
finite set of possible values, a time-forwards Markov process splits the set
of possible values into two subsets — the set of transient states (where
probability always goes to zero, regardless of initial state) and of ergodic
states. The ergodic core of this process — the process
restricted to the ergodic states — can be represented equivalently as
a time-forwards, time-backwards and mixed forwards-backwards MRF, in a driver
representation, and it admits a neighborhood representation. But the presence
of transient states (boundary conditions) in any of these three situations
destroys any possibility of such equivalence or of a neighborhood representation;
it is like nonstationarity in statistics.
is taken from a
finite set of possible values, a time-forwards Markov process splits the set
of possible values into two subsets — the set of transient states (where
probability always goes to zero, regardless of initial state) and of ergodic
states. The ergodic core of this process — the process
restricted to the ergodic states — can be represented equivalently as
a time-forwards, time-backwards and mixed forwards-backwards MRF, in a driver
representation, and it admits a neighborhood representation. But the presence
of transient states (boundary conditions) in any of these three situations
destroys any possibility of such equivalence or of a neighborhood representation;
it is like nonstationarity in statistics.
5. Discussion - The role of mesoscopic elements in biocomplexity
For heuristic purposes we define an intermediate level of brain function between single neurons or sparse networks of dendritic bundles and cortical columns operating at a microscopic level, and those large brain parts whose activities are observed with scalp EEG, fMRI, PET, and comparable optical imaging techniques in humans. We find it necessary to introduce the mesoscopic level to interpret data taken with 8x8 arrays of electrodes over cortical surfaces (Freeman, 1992; Barrie, Freeman and Lenhart, 1996). These domains having diameters of 0.5 to 2 cm are much larger than columns, barrels and glomeruli, but they are at or below the lower limits of spatial resolution by macroscopic methods. Their properties are determined by the self-organizing chaotic dynamics of local populations of neurons, in which the delays introduced by the conduction velocities of the axons of participating neurons provide the limitations on mesoscopic sizes and durations.
Mesoscopic effects operating at spatial and temporal scales of 1 cm and 100 ms mediate between the two extremes of single neurons and the major lobes of the forebrain. They correspond in size to Brodmann's areas and in duration to psychophysical events that compose perceptions. Mesoscopic effects provide a link between extreme local fragmentation and global uniformity. They change continually in space and time, requiring a very close relationship between dynamic events, e.g., EEG bursts, and the media through which the propagation occurs. This requires a nonlinear approach, see (Skarda and Freeman, 1987; Freeman, 1992). In physics the importance of intermediate-range effects is well recognized (Kozma, 1998; Gade and Hu, 1999).
We illustrate the problem with Nunez' ocean wave analogy (Nunez, 2000; Freeman and Kozma, 2000). Propagation of such waves leaves largely unchanged the properties of the water through which transmission takes place. In mathematics the linearity of a 2nd order PDE formalizes this independence. Neural tissues are not passive media through which effects propagate as waves do in air and water. Extensive interactions between the propagating signal and the neural tissue, however, reveal that nonlinear effects are essential in brains, in which the dynamics is inseparable from the medium. The brain medium itself has an intimate relationship with the dynamics. There is a continuous excitation in the neural tissue, usually in sub-threshold regimes. Occasionally due to external stimuli, for example, the activity crosses a threshold. At that point the properties of the medium drastically change in a phase transition to accommodate changed external conditions. Mesoscopic elements are needed to introduce these nonlinearities, which are the essence of adaptation through perception and learning.
Conventional thermodynamics starts out by using very solid, reasonable and useful concepts about ergodic systems. In the rigorous concepts, one can measure relative entropy of a specified probability distribution relative to the stable equilibrium distribution. The "entropy" function is essentially just the logarithm of the invariant probability measure, which is simply the stable equilibrium probability distribution of possible states of the system. It is assumed that the entropy function of the universe is local and that it can be represented as the SUM of local entropy over all objects in the universe. Finally, it is assumed that the local entropy of an object is a function solely of the state of that object. This is equivalent to assuming that there never will be correlations across state in equilibrium -- an indefensible a priori assumption! When one enforces that assumption, one can "deduce" that life will not exist in equilibrium... that only the "heat death" can ever survive in equilibrium in any universe. All by assumption. In this work we are interested in how to get beyond the locality assumption, how to develop some sorts of mathematical tools to deal with the entropy functions which lead to phenomena like life.
Neurobiological observations provide a clue is this respect. What distinguishes brain chaos from other kinds is the filamentous texture of neural tissue called neuropil, which is unlike any other substance in the known universe (Freeman, 1995). Neural populations stem ontogenetically in embryos from aggregates of neurons that grow axons and dendrites and form synaptic connections of steadily increasing density. At some threshold the density allows neurons to transmit more pulses than they receive, so that an aggregate undergoes a state transition from a zero point attractor to a non-zero point attractor, thereby becoming a population. Mathematically such a property has been described in random graphs, where the connectivity density is an order parameter that can induce state transitions, (Erdos and Renyi, 1960; Bollobas, 1985; Kauffman, 1995). Accordingly, state transitions in neuronal populations can be interpreted as a kind of percolation phenomenon in the neurophil medium. The dendritic currents of single neurons that govern pulse frequencies sum their potential fields in passing across the extracellular resistance, giving rise to extraneuronal potential differences manifested in the EEG, which correspond to the local mean fields of pulse densities in neighborhoods of neurons contributing to the local field potentials. In early stages of development these fields appear as direct current "d.c." fields with erratic fluctuations in the so-called "delt" range < 1 Hz. The neurons are excitatory, and their mutual excitation provides the sustained aperiodic activity that neurons require to stay alive and grow.
Unlike transistors, neurons have a short shelf life if they are isolated and left inactive. The activity of an excitatory population is self-stabilized by a non-zero point attractor (Freeman, 1975), giving rise to a field of nearly white noise, up to a frequency limit determined by the duration of the action potentials. The feedback can be modeled as a one-dimensional diffusion process, which randomizes the input of each neuron with respect to others' output and its own output. At some later stage, typically in humans after birth, cortical inhibitory neurons develop or transform from excitatory neurons, which contribute negative feedback, leading to the appearance of oscillations in the gamma spectrum of the EEG. The mutual excitation persists, and, in fact, is essential for the maintenance of the near-linear range of cortical oscillations through a depolarizing bias.
6. Concluding remarks
Our research aims at establishing methodological foundations of biocomplexity, its mathematical and computational aspects. We also demonstrate the application of the methodology on the example of sensory information processing. The intellectual challenge associated with the introduction of computational principles based on the newly developed theory of biocomplexity using stochastic chaos approach is enormous. It requires revisiting analytical tools of scientific research used in the modern ages, started with the Newtonian revolution. The major goal of this work is to show that there is a potential to overcome the shortcomings of the reductionist approach by laying down firm mathematical and methodological foundations of a new discipline at the interface of stochastic processes and dynamical systems. Our experience with sensory information processing seems very useful in this respect, as the very existence of biological systems roots in their continuous interaction with the environment via sensory channels and the closely related feedback loop created by their actions. The present work is a step towards establishing methodological foundations of non-autonomous dynamical systems.
Acknowledgments: This work was supported in part by ARO MURI grant DAAH04-96-1-0341 and by NIMH grant MH06686.
8. References
1. Aihara, K., Takabe T., Toyoda M., 1990. Chaotic neural networks, Phys. Lett. A, 144 (6-7), 333-340.
2. Andreyev, Y.V., Dmitriev, A.S., Kuminov D.A., 1996. 1-D maps, chaos and neural networks for information processing, Int. J. Bifurcation & Chaos, 6(4), 627-646.
3. Aradi, I., Barna G., Erdi P., 1995. Chaos and learning in the olfactory bulb, Int. J. Intel. Syst., 10(1), 89-117.
4. Assumian, R.D., Moss F. et al.., 1998. The constructive role of noise in fluctuation driven transport and stochastic resonance, Chaos, 8(3), 533-628.
5. Babloyantz, A., and Desthexhe A., 1986. Low-dimensional chaos in an instance of epilepsy, Proc. Natl. Acad. Sci. USA, 83, 3513-3517.
6. Barrie, J.M., Freeman, W.J., Lenhart, M.D., 1996. Spatiotemporal analysis of prepyriform, visual, auditory, and somesthetic surface EEGs in trained rabbits, J. Neurophysiology, 76(1), 520-539.
7. Bollobas, B., 1985. Random Graphs, 1985. London ; Orlando : Academic Press.
8. Borisyuk, R.M., Borisyuk G.N., 1997. Information coding on the basis of synchronization of neuronal activity, Biosystems, 40(1-2), 3-10.
9. Box, G.E.P., and Jenkins, G.M., 1970. Time-series analysis: Forecasting and control, Holden-Day.
10. Brown, R., and Chua L., 1999. Clarifying Chaos 3. Chaotic and stochastic processes, chaotic resonance and number theory, Int. J. Bifurcation & Chaos, 9, 785-803.
11. Bulsara, A., Elston T.C., Doering C.R. et al., 1991. Cooperative behavior in periodically driven noisy integrate-fire models of neuronal dynamics, Phys. Rev. E, 53(4), Part B, 3958-69.
12. Chang, H.J., Freeman W.J., Burke B.C., 1998. Optimization of olfactory model in software to give 1/f power spectra reveals numerical instabilities in solutions governed by aperiodic (chaotic) attractors, Neur. Netw., 11, 449-466.
13. ChapeauBlondeau, F. and Godivier X., 1996. Stochastic resonance in nonlinear transmission of spike signals — An exact model and application to the neuron, Int. J. Bifurcation & Chaos, 6(11), 2069-2076.
14. Chate, H. and Manneville, P., 1992. Collective behaviors in spatially extended systems with local interactions and synchronous updating, Progr. Theor. Phys., 87(1), 1-60.
15. Chate, H., 1995. On the analysis of spatio-temporally chaotic data, Physica D, 86 (1-2) 238-247.
16. Chate, H., A. Lemaitre, P. Marcq, P. Manneville, 1996. Non-trivial collective behavior in extensively-chaotic dynamical systems: An update, Physica A, 224, 447-457.
17. Csilling, A., I.M. Janosi, G. Pasztor, I. Scheuring, 1994. Absence of chaos in a self-organized critical coupled map lattice, Phys. Rev. E, 50, 1083-1092.
18. El-Karoui, N. & L.Mazliak (eds.) 1997. Backward stochastic differential equations, Addison-Wesley.
19. Erdos, P. and Renyi A., 1960. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5: 17-61.
20. Freeman, W.J., 1975. Mass Action in the Nervous System, Academic Press, New York.
21. Freeman, W.J., 1992. Tutorial on neurobiology - From single neurons to brain chaos, Int. J. Bifurcation & Chaos, 2(3), 451-482.
22. Freeman W.J.,1995. Societies of Brains. Mahwah: NJ, Lawrence Erlbaum Associates.
23. Freeman, W.J., 2000. A proposed name for aperiodic brain activity: stochastic chaos, Neural Networks, 13, 11-13.
24. Freeman, W.J., 2000a. Neurodynamics. An Exploration to Mesoscopic Brain Dynamics. London, UK: Springer-Verlag.
25. Freeman, W.J., H.J. Chang, et al., 1997. Taming chaos: Stabilization of aperiodic attractors by noise, IEEE Trans. Circ. Syst. — I. Fundamental Theory & Appl., 44(10), 989-996.
26. Freeman WJ and Kozma, R., 2000. Local-global interactions and the role of mesoscopic (intermediate range) elements in brain dynamics. Behavioral and Brain Sciences, 23(3).
27. Gade, P.M. & C.K. Hu, 1999. Synchronization and coherence in thermodynamic coupled map lattices with intermediate-range coupling, Phys. Rev. E, 60(4), 4966-4969.
28. Gammaitoni, L., Hanggi P., Jung P., Marchesoni F., 1998. Stochastic resonance, Rev. Mod. Phys. 70(1), 223-287.
29. Haken H, 1991. Synergetic Computers and Cognition. Berlin: Springer-Verlag.
30. Hirsch, M.W., 1989. Convergent activation dynamics in continuous time neural networks, Neur. Netw., 2, 331-351.
31. Hirsch, M.W., 1996. Mathematics of Hebbian Attractors, Behavioral & Brain Sci., 18, 633-34.
32. Ishii, S., Fukumizu K., Watanabe S., 1996. A network of chaotic elements for information processing, Neur. Netw., 9(1), 25-40.
33. Jordan, M., 1998. Learning in graphical models, Kluwer Academic.
34. Kaneko, K., 1990. Clustering, coding, switching, hierarchical ordering, and control in a network of chaotic elements, Physica D, 41, 137-172.
35. Kaneko, K. (ed.), 1993. Theory and Applications of Coupled Map Lattices, Wiley, New York.
36. Kaneko, K., 1997. Dominance of Milnor attractors and noise-induced selection in a multiattractor system. Phys. Rev. Lett., 78, 2736-2739.
37. Kaneko, K., 1998. On the strength of attractors in a high-dimensional system: Milnor attractor network, robust global attraction, and noise-induced selection. Physica D, 124, 308-330.
38. Kauffman, S.A., 1990. Requirements for evolvability in complex systems: orderly dynamics and frozen components, Physica D, 42, 135-152.
39. Konno, H.; Kozma, R.; Kitamura, M., 1996. CML approach to power reactor dynamics. I. Preservation of normality, Ann. Nucl. Energy, 23 (2), 119-31.
40. Kozma, R., Sakuma, M., Yokoyama, Y., Kitamura, M., 1996. On the Accuracy of Mapping by Neural Networks Trained by BP with Forgetting, Neurocomputing, 13, 295-311.
41. Kozma, R., 1997. Multi-level knowledge representation in neural networks with adaptive structure, Int. J. Syst. Res. & Info. Sci., 7, 147-167.
42. Kozma, R., 1998. Intermediate range coupling generates low-dimensional attractors deeply in the chaotic region of one-dimensional lattices, Phys. Lett. A, 244, 85-91.
43. Kozma, R. and Freeman, W.J., 1999. A possible mechanism for intermittent oscillations in the KIII model of dynamic memories - the case study of olfaction, Proc. IJCNN’99, Washington D.C., July 10-16, Vol. 1, 52-57.
44. Kozma R. and Freeman, W.J., 2000a. Encoding and recall of noisy spatio-temporal memory patterns in the style of brains, Proc. 2000 Int. Joint Conf. Neural Networks, Vol. 5, 33-38.
45. Kozma, R. and Freeman W.J., 2000b. Knowledge acquisition in connectionist systems via crisp, fuzzy and chaos methods, Eds. M.L. Padgett, N.B. Karayiannis, L.A. Zadeh, CRC Handbook of Applied Computational Intelligence, CRC Press (in press).
46. Kozma, R. and Freeman, W.J., 2001. Chaotic Resonance - Methods and applications for robust classification of noisy and variable patterns, Int. J. Bifurcation & Chaos, 11(6), June, 2001 (in press).
47. Kuramoto Y. and Nakao, H., (1996) Origin of power-law spatial correlations in distributed oscillators and maps with nonlocal coupling, Phys. Rev. Lett. 76, 4352-4355.
48. Kuramoto Y. and Nakao, H., (1997) Power-law spatial correlations and the onset of individual motions in self-oscillatory media with non-local coupling, Physica D, 103, 294-313.
49. Levin, J.E. & Miller J.P., 1996. Broadband neural encoding in the cricket cercal sensory system enhanced by stochastic noise, Nature, 380, 165-168.
50. Minai, A.A., Anand T., 1998. Stimulus induced bifurcations in discrete-time neural oscillators, Biol. Cyb., 79(1), 87-96.
51. Mitaim, S. and Kosko B., 1998. Adaptive stochastic resonance, Proc. IEEE, 86(11) 2152-2183.
52. Moss, F. and Pei X., 1995. Stochastic resonance — Neurons in parallel, Nature, 376, 211-212.
53. Nakagawa, M., 1998. Chaos associative memory with a periodic activation function, J. Phys. Soc. Japan, 67(7), 2281-2293.
54. Nunez, P. L., 2000. Toward a Quantitative Description of Large Scale Neocortical Dynamic Function and EEG, Behavioral & Brain Sci., 23 (3).
55. Penrose, R., 1994. Shadows of the mind, London: Oxford Press.
56. Perez G., Pando-Lambruschini C., Sinha S., Cerdeira J..A., 1992. Nonstatistical behavior of coupled optical systems, Phys. Rev. A, 45: (8) 5469-5473.
57. Perez, G., Sinha, S., Cerdeira, H. A., 1993. Order in the turbulent phase of globally coupled maps, Physica D, 63, 341-349.
58. Perrone, A.L. & Basti G., 1995. Neural images and neural coding, Behavioral & Brain Sci., 18 (2), 368-369.
59. Prigogine I., 1980. From Being to Becoming: Time and Complexity in the Physical Sciences. San Francisco: Freeman.
60. Rapp, P., 1993. Chaos in the neurosciences: Cautionary tales from the frontier. Biologist, 40, 89-94.
61. Roy, M.; Amritkar, R.E., 1997. Observation of stochastic coherence in coupled map lattices. Phys. Rev. E, 55 (3A), 2422-5.
62. Sbitnev, V.I., 1997. Noise induced phase transition in a two-dimensional coupled map lattice. Complex Systems, 11(4), 309-21.
63. Schiff, S.J. et al., 1994. Controling chaos in the brain, Nature, 370, 615-620.
64. Schuster, H.G. & Stemmler, 1997. Control of chaos by oscillating feedback, Phys. Rev. E, 56(6), 6410-6417.
65. Sinha, S., Biswas, D., Azam, M., Lawande, S.V., 1992. Local-to-global coupling in chaotic maps, Phys. Rev. A, 46, 6242-6246.
66. Sinha, S., 1998. Roughening of spatial profiles in the presence of parametric noise. Phys. Lett. A, 245 (5), 393-8.
67. Skarda, C.A. and Freeman W.J., 1987. How brains make chaos in order to make sense of the world, Behavioral & Brain Sci., 10, 161-195.
68. Turing A.M., 1952. The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society 237B: 37-72.
69. Tsuda, I., 1992. Dynamic link of memory — Chaotic memory map in nonequilibrium neural networks, Neur. Netw., 5, 313-326.
70. Tsuda, I., 1994. Can stochastic renewal maps be a model for cerebral cortex, Physics D, 75 (1-3), 165-178
71. Tsuda, I., 2001. Towards an interpretation of dynamic neural activity in terms of chaotic dynamical systems, Behavioral and Brain Sci., 24(4) (in press).
72. Von Neumann, J., 1958. The Computer and the Brain. New Haven CT: Yale University Press.
73. Wang, L.P., 1996. Oscillatory and chaotic dynamics in neural networks under varying operating conditions, IEEE Trans. Neur. Netw., 7(6), 1382-1388.
74. Werbos, P.J., 1989. Bell's theorem: the forgotten loophole and how to exploit it, In M.Kafatos, ed., Bell's theorem, quantum theory and conceptions of the Universe, Kluwer.
75. Werbos, P.J., 1992. Neurocontrol and supervised learning — an overview and evaluation, in "Handbook of Intelligent Control," D.A. White & D.A.Sofge (eds.), 65-89.
76. Werbos, P.J., 1994. Self-organization: Re-examining the basics and an alternative to Big Bang, In: Pribram K. (ed.), Origins: Brain and Self-Organization, Erlbaum.
77. Werbos, P.J., 1998. New approaches to soliton quantization and existence in particle physics, xxx.lanl.gov/abs/patt-sol/9804003 , Sec.3.
78. Werbos, P.J., 1999. Can solitons attractors exist in realistic 3+1 D conservative systems? Chaos, Solitons and Fractals, 10(11).
79. Werbos, P.J., 2000. Extending chaos and complexity theory to address life, brain, and quantum foundations, Proc. IJCNN'2000, July 24-27, 2000, Como, Italy.
80. Yao, and Freeman, W.J., 1990. Model of biological pattern recognition with spatially chaotic dynamics, Neur. Netw., 3 (2) 153-170.
81. Zak M., 1993. Terminal model of Newtonian dynamics. International J. Theoretical Physics 32: 159-190.
82. Zinn-Justin, J., 1996. Quantum field theory and critical phenomena, 3rd ed., Oxford U. Press.


Figures:

21st, The VXM Network, https://vxm.com